مساحت دایره: فرمول. چرا مساحت دایره در مربعی برابر با مثلث متساوی الساقین قائم الزاویه، ذوزنقه قائم الزاویه و متساوی الساقین توصیف و حک شده است؟

چگونه مساحت دایره را پیدا کنیم؟ ابتدا شعاع را پیدا کنید. یاد بگیرید که کارهای ساده و پیچیده را حل کنید.

دایره یک منحنی بسته است. هر نقطه روی خط دایره از نقطه مرکزی فاصله خواهد داشت. دایره یک شکل مسطح است، بنابراین حل وظیفه یافتن مساحت ساده است. در این مقاله نحوه یافتن مساحت دایره ای که در یک مثلث، ذوزنقه، مربع و در نزدیکی این شکل ها شرح داده شده است را در نظر خواهیم گرفت.

مساحت دایره: فرمول با استفاده از شعاع، قطر، طول دایره، مثال‌های حل مسئله

برای یافتن مساحت یک شکل، باید بدانید که شعاع، قطر و عدد π است.

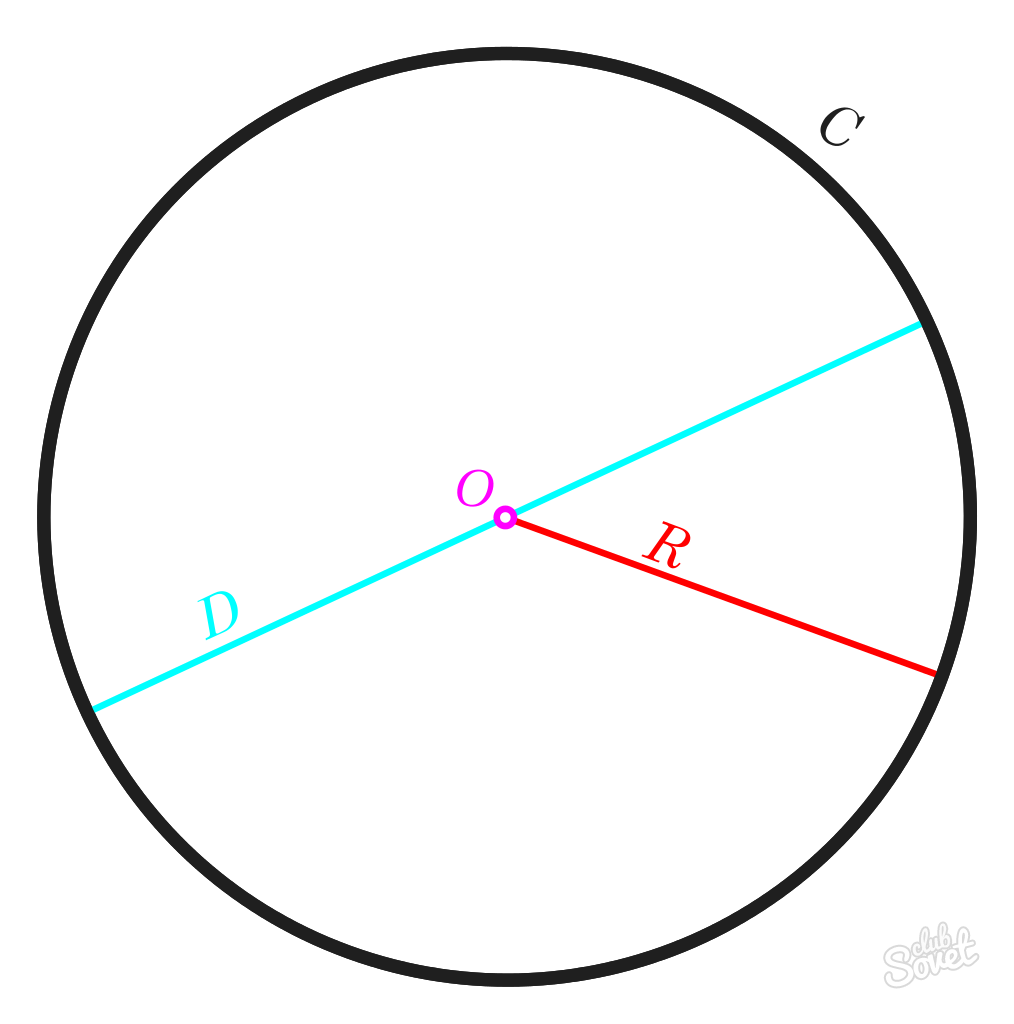
شعاع R فاصله محدود شده توسط مرکز دایره است. طول تمام شعاع های R یک دایره برابر خواهد بود.

قطر D خطی بین هر دو نقطه روی دایره ای است که از نقطه مرکزی می گذرد. طول این قطعه برابر است با طول شعاع R ضرب در 2.

عدد π یک مقدار ثابت برابر با 3.1415926 است. در ریاضیات معمولاً این عدد به 3.14 گرد می شود.

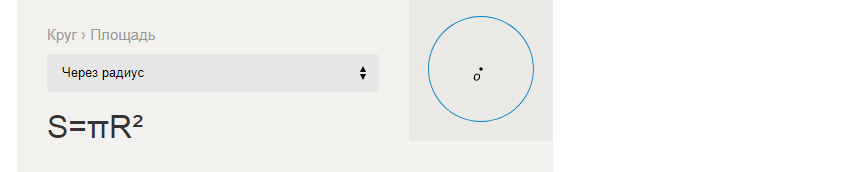
فرمول برای یافتن مساحت یک دایره از طریق شعاع:

نمونه هایی از حل وظایف برای یافتن ناحیه S یک دایره از طریق شعاع R:

---------- ---------------------------- --

وظیفه: اگر شعاع دایره ای 7 سانتی متر باشد، مساحت دایره را بیابید.

راه حل: S=πR2، S=3.14*72، S=3.14*49=153.86 cm2.

پاسخ: مساحت دایره 153.86 سانتی متر مربع است.

فرمول برای یافتن مساحت S یک دایره از طریق قطر D:

نمونه هایی از حل تکالیف برای یافتن S اگر D مشخص باشد:

]

--------- ---------------------------------

جستجو: S یک دایره را پیدا کنید، اگر D آن برابر با 10 سانتی متر باشد.

راه حل: P=π*d2/4، P=3.14*102/4=3.14*100/4=314/4=78.5 سانتی متر مربع.

پاسخ: مساحت یک شکل گرد صاف 78.5 سانتی متر مربع است.

یافتن S یک دایره، اگر طول دایره مشخص باشد:

ابتدا، شعاع آن را می‌یابیم. طول دایره با فرمول محاسبه می شود: L=2πR، بر این اساس، شعاع R برابر با L/2π خواهد بود. اکنون مساحت دایره را با استفاده از فرمول از طریق R پیدا می کنیم.) ----------- -----------------------------

وظیفه: مساحت یک دایره را بیابید، اگر طول دایره L مشخص باشد - 12 سانتی متر.

راه حل: ابتدا شعاع را پیدا می کنیم: R=L/2π=12/2*3.14=12/6.28=1.91.

اکنون مساحت را از طریق شعاع پیدا می کنیم: S=πR2=3.14*1.912=3.14*3.65=11.46 cm2.

پاسخ: مساحت دایره 11.46 سانتی متر مربع است.

مساحت دایره محاط شده در مربع: فرمول، نمونه هایی از حل مسائل

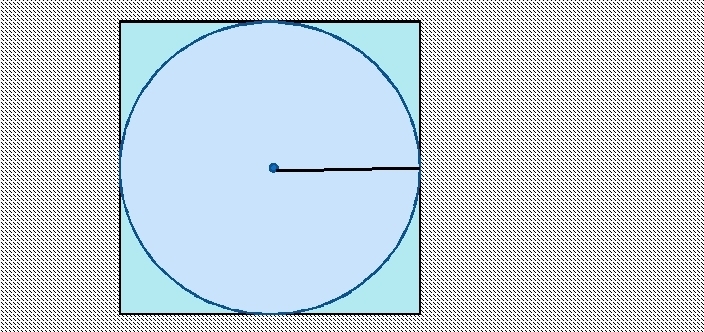
یافتن مساحت دایره ای که در یک مربع محاط شده است ساده است. ضلع مربع قطر دایره است. برای پیدا کردن شعاع، باید ضلع را بر 2 تقسیم کنید.)

نمونه هایی از حل مسائل برای یافتن مساحت دایره محاط شده در یک مربع:

---------------------------------- ----

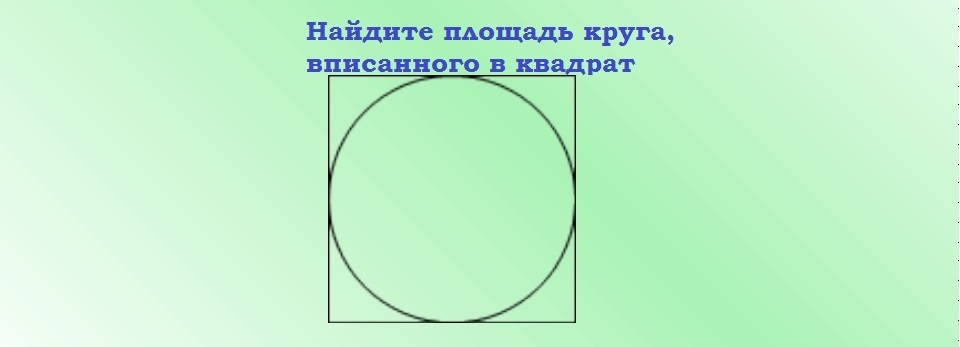
کار شماره 1: ضلع یک شکل مربع که برابر با 6 سانتی متر است مشخص است.ناحیه S دایره محاط شده را پیدا کنید.

راه حل: S=π(a/2)2=3.14(6/2)2=3.14*9=28.26 cm2.

پاسخ: مساحت یک شکل گرد صاف 28.26 سانتی متر مربع است.

----------------------------------------- -----------

کار شماره 2 :S از دایره ای را بیابید که به شکل مربع محاط شده است و شعاع آن اگر یک ضلع برابر با a=4 باشد را ببینید

به صورت زیر حل کنید : ابتدا R=a/2=4/2=2 را پیدا می کنیم.

اکنون مساحت دایره S=3.14*22=3.14*4=12.56 cm2 را خواهیم یافت.

پاسخ: مساحت یک شکل گرد صاف 12.56 سانتی متر مربع است.

مساحت یک دایره محصور در اطراف یک مربع: فرمول، نمونه هایی از حل مسائل

یافتن مساحت شکل گرد توصیف شده در اطراف یک مربع کمی دشوارتر است. اما با دانستن فرمول، می توانید به سرعت این مقدار را محاسبه کنید.

فرمول برای یافتن S از یک دایره محصور در اطراف یک شکل مربع:

نمونه هایی از حل مسائل برای یافتن مساحت یک دایره توصیف شده در اطراف یک شکل مربع:

) مسئله

مساحت دایره محاط شده در مثلث قائم الزاویه و متساوی الساقین: فرمول، نمونه هایی از حل مسائل

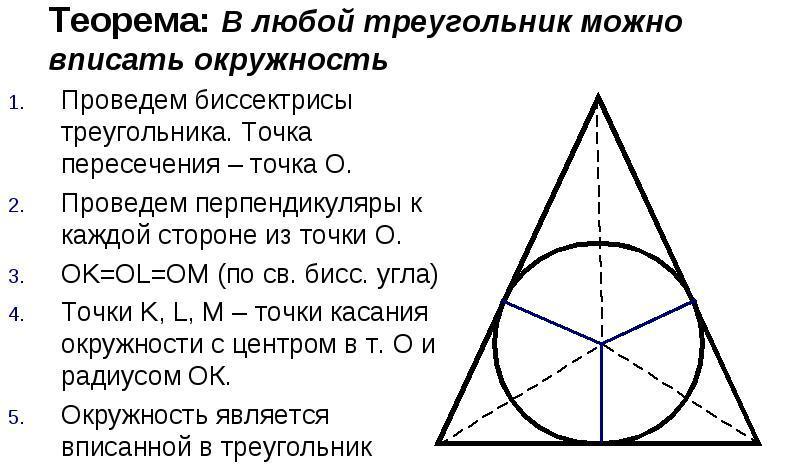
دایره‌ای که در شکل مثلثی حک شده است، دایره‌ای است که هر سه ضلع مثلث را لمس می‌کند. هر شکل مثلثی را می توان با یک دایره حک کرد، اما فقط یک دایره. مرکز دایره نقطه تقاطع نیمسازهای زاویه مثلث خواهد بود.

فرمول برای یافتن مساحت دایره محاط شده در مثلث متساوی الساقین:

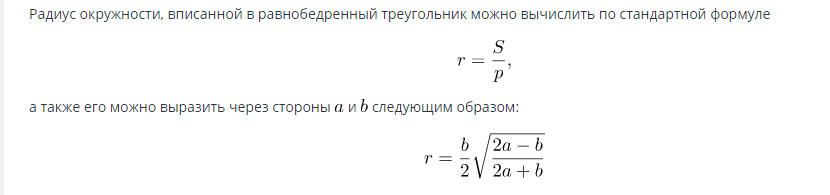
هنگامی که شعاع مشخص است، مساحت را می توان با استفاده از فرمول محاسبه کرد: S=πR2.

فرمول برای یافتن مساحت دایره محاط شده در مثلث قائم الزاویه:

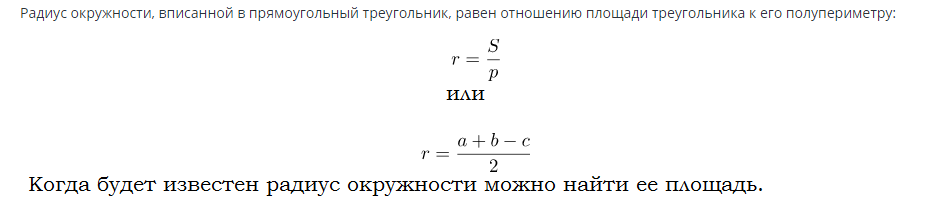
نمونه هایی از راه حل های مسئله:

مشکل شماره 1

)

اگر در این مسئله نیز باید مساحت دایره ای با شعاع 4 سانتی متر را پیدا کنید، می توانید این کار را با فرمول انجام دهید: S=πR2

کار شماره 2

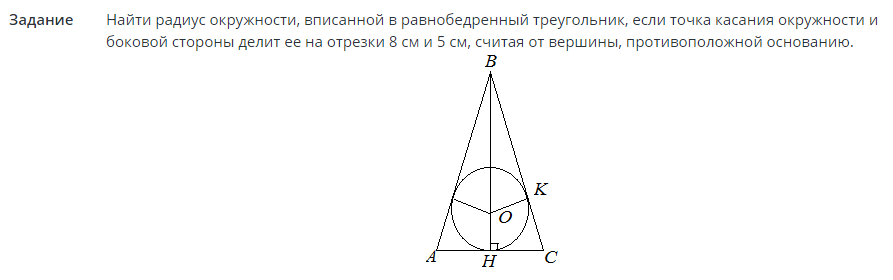
راه حل:

اکنون که شعاع مشخص شده است، مساحت دایره را می توان بر حسب شعاع پیدا کرد. فرمول بالا را در متن ببینید.

کار شماره 3

]

مساحت دایره ای که پیرامون یک مثلث قائم الزاویه و متساوی الساقین محصور شده است: فرمول، نمونه هایی از حل مسائل

همه فرمول ها برای پیدا کردن مساحت یک دایره به این واقعیت ختم می شود که ابتدا باید شعاع آن را پیدا کنید. هنگامی که شعاع مشخص است، پیدا کردن منطقه ساده است، همانطور که در بالا توضیح داده شد.

​​

مساحت یک دایره محصور در اطراف یک مثلث قائم الزاویه و متساوی الساقین با فرمول زیر پیدا می شود:

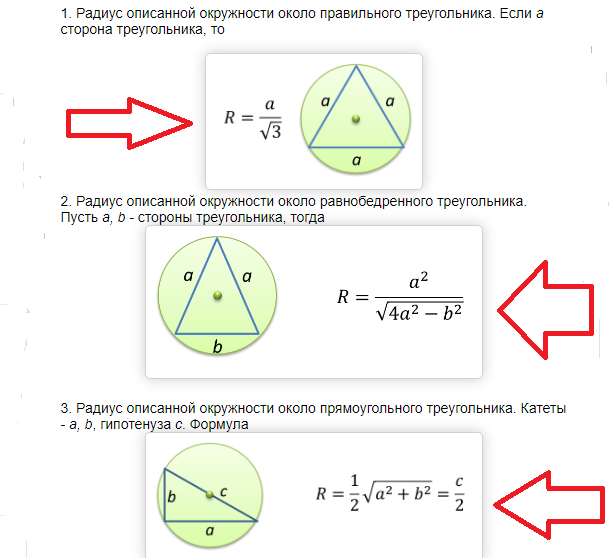
نمونه هایی از حل مسئله:

در اینجا مثال دیگری از حل یک مشکل استفاده از فرمول هرون

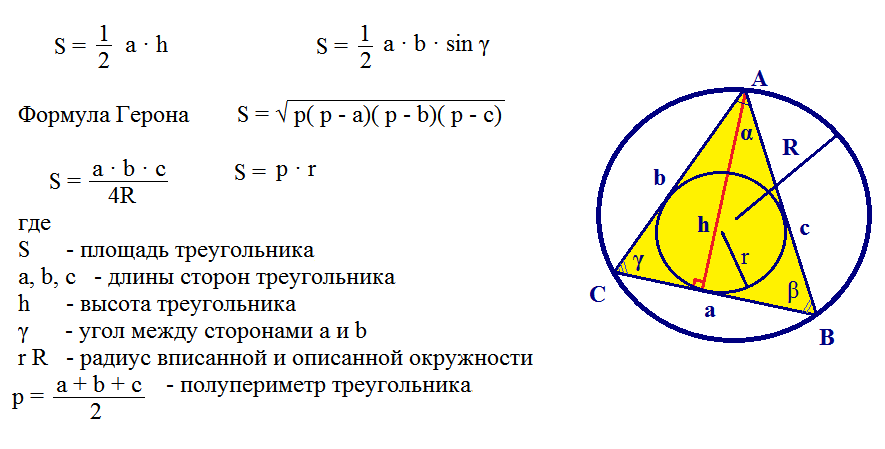
حل آن دشوار است مشکلات مشابه، اما اگر همه فرمول ها را بدانید می توان بر آنها غلبه کرد. دانش آموزان در کلاس نهم چنین وظایفی را حل می کنند.

مساحت دایره ای که در یک ذوزنقه مستطیلی و متساوی الساقین حک شده است: فرمول، مثال های حل مسئله

به عنوان مثال، یک ذوزنقه متساوی الساقین با یک حک شده است. دایره ای که در نقطه تماس قرار دارد یک طرف را به قطعات m و n تقسیم می کند.

برای حل این مشکل، باید از فرمول های زیر استفاده کنید:

یافتن مساحت یک دایره حک شده در ذوزنقه مستطیلی مطابق فرمول زیر انجام می شود:

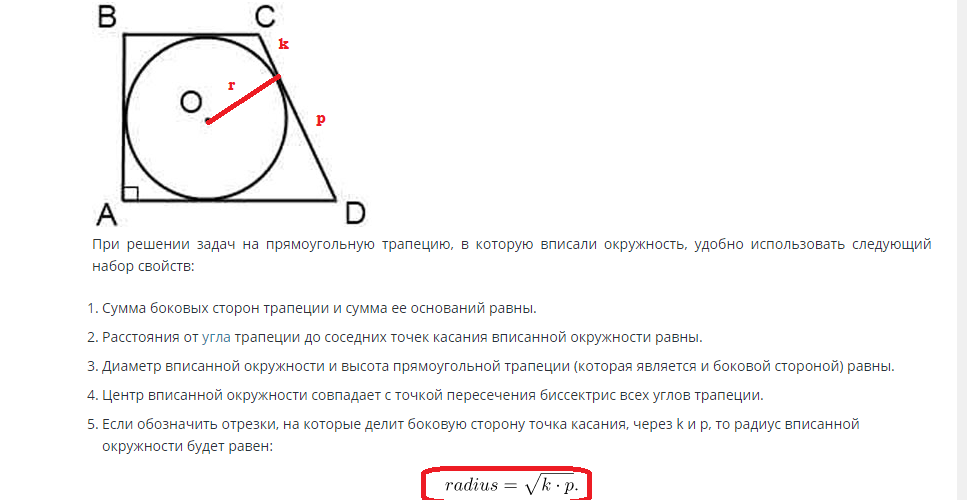
اگر ضلع مشخص باشد، شعاع را می توان از طریق این مقدار پیدا کرد. ارتفاع ضلع ذوزنقه برابر با قطر دایره و شعاع آن نصف قطر است. بر این اساس، شعاع برابر با R=d/2 است.

نمونه هایی از حل مسائل:

مساحت دایره ای که پیرامون یک ذوزنقه قائم الزاویه و متساوی الساقین احاطه شده است: فرمول، مثال های حل مسئله

ذوزنقه را می توان حک کرد در دایره ای که مجموع زوایای مقابل 180 درجه باشد. بنابراین، فقط ذوزنقه متساوی الاضلاع را می توان نوشت. شعاع محاسبه مساحت دایره ای که در نزدیکی یک ذوزنقه مستطیلی یا متساوی الساقین توصیف شده است با استفاده از فرمول های زیر محاسبه می شود: و ذوزنقه متساوی الساقین: فرمول، نمونه هایی از حل مسئله

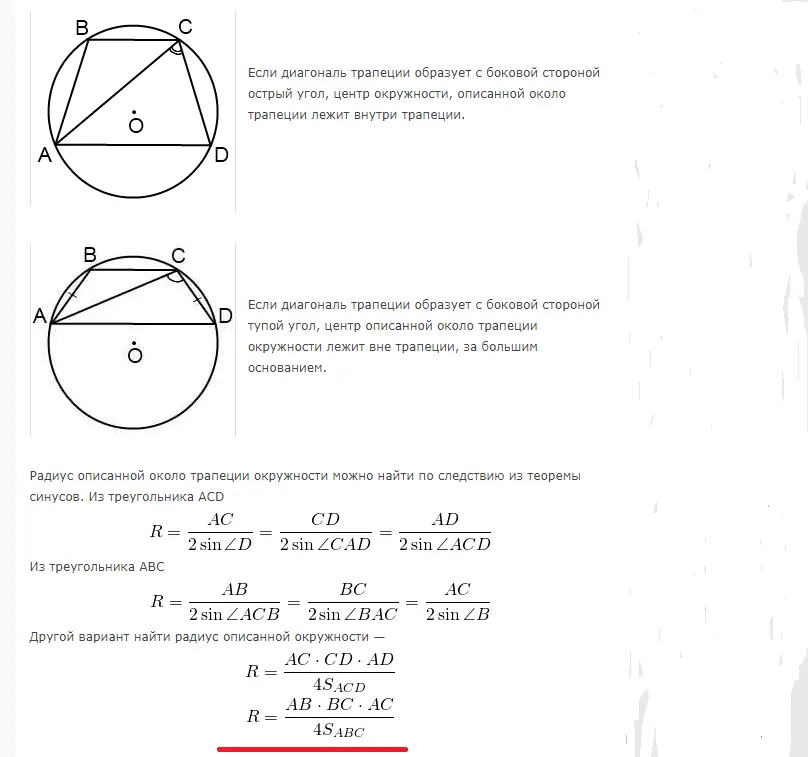
نمونه هایی از حل مسئله:

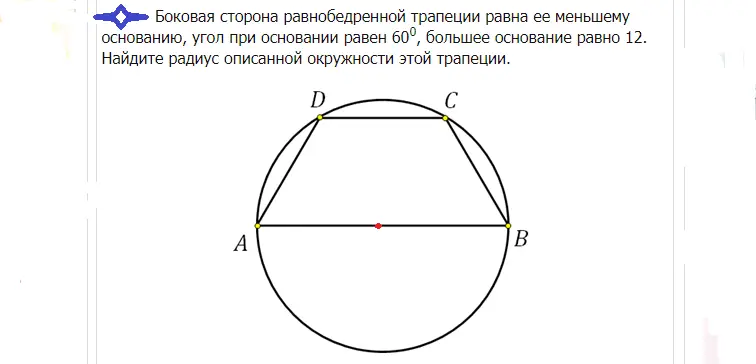
راه حل: قاعده بزرگ در این حالت از مرکز می گذرد، زیرا ذوزنقه ای متساوی الساقین در دایره حک شده است. مرکز این پایه را دقیقاً به نصف تقسیم می کند. اگر پایه AB برابر با 12 باشد، شعاع R را می توان به صورت زیر یافت: R=12/2=6.

پاسخ: شعاع 6 است.

در هندسه، دانستن فرمول ها مهم است. اما به خاطر سپردن همه آنها غیرممکن است، بنابراین حتی در بسیاری از امتحانات مجاز به استفاده از یک فرم خاص است. با این حال، یافتن فرمول مناسب برای حل این یا آن مشکل مهم است. حل مسائل مختلف برای یافتن شعاع و مساحت یک دایره را تمرین کنید تا بتوانید فرمول ها را به درستی جایگزین کنید و پاسخ های دقیق دریافت کنید.

ویدئو: ریاضیات | محاسبه مساحت های دایره و اجزای آن